2.1 numeric、boolean
#
一、boolean
#
源码
#
1
2
3
4
5
6
7
8
9
10
| // go/src/builtin/builtin.go
// bool is the set of boolean values, true and false.
type bool bool
// true and false are the two untyped boolean values.
// **自引用定义的方式:通过逻辑表达式来定义布尔值本身**
const (
true = 0 == 0 // Untyped bool. 类型是:**无类型布尔值**,值是:0 == 0的结果是true。无类型布尔值可以赋值给任何布尔类型
false = 0 != 0 // Untyped bool.
)
|
源码解读
#
值只有true和false,!true的值为false,且==和<等比较操作也会产生布尔型的值。
布尔值可以和&&(AND)和||(OR)操作符结合,并且有短路行为(不再对运算符右边表达式求值)。所以 s != "" && s[0] == 'x' 不会导致数组越界panic异常。&&(对应逻辑乘法) 优先级高于 ||(对应逻辑加法),所以不需要小括号
1
2
3
4
5
| if 'a' <= c && c <= 'z' ||
'A' <= c && c <= 'Z' ||
'0' <= c && c <= '9' {
// ...ASCII letter or digit...
}
|
布尔值并不会隐式转换为数字值0或1,反之亦然。需要显式的if语句辅助转换:
二、number
#
整型
#
有符号整数采用2的补码形式表示,也就是最高bit位用来表示符号位,一个n-bit的有符号数的值域是从-2^{n-1}到2^{n-1}-1。
无符号整数的所有bit位都用于表示非负数,值域是0到2^{n}-1。
1
2
3
4
5
6
7
8
9
10
11
12
| // type test
package main
import "fmt"
func main() {
bytes := []byte("hello")
s := "hello"
fmt.Println(bytes) // [104 101 108 108 111] h的ascii码的十进制表示为104,e的ascii码的十进制表示为101,以此类推
fmt.Printf("%b\n", bytes) // [1101000 1100101 1101100 1101100 1101111]
fmt.Printf("%b\n", s) // %!b(string=hello) wrong type
}
|
Go语言中关于算术运算、逻辑运算和比较运算的二元运算符共有5种优先级,在同一个优先级使用左优先结合规则,但使用括号可以明确优先顺序和提升优先级:
1
2
3
4
5
6
| // 二元运算符有五种优先级。。如mask & (1 << 28)
优先级1: * / % << >> & &^ // 乘除类
优先级2: + - | ^ // 加减类
优先级3: == != < <= > >= // 比较类
优先级4: && // 逻辑乘法
优先级5: || // 逻辑加法
|
算术运算符+、-、*和/可以适用于整数、浮点数和复数,但是取模运算符%仅用于整数间的运算。
在Go语言中,%取模运算符的符号和****被取模数(前1个数)的符号一致的,因此-5%3和-5%-3结果都是-2。(不同编程语言,%取模运算的行为可能并不相同。)
除法运算符/的行为则依赖于操作数是否全为整数,比如5.0/4.0的结果是1.25,但是5/4的结果是1,因为整数除法会向着0方向截断余数。
一个算术运算的结果,不管是有符号或者是无符号的,如果需要更多的bit位才能正确表示的话,就说明计算结果是溢出了,超出的高位的bit位部分将被丢弃。如果原始的数值是有符号类型,而且最左边的bit位是1的话,那么最终结果可能是负的,例如int8的例子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| // type test
package main
import "fmt"
func main() {
bytes := []byte("hello")
s := "hello"
fmt.Println(bytes) // [104 101 108 108 111] h的ascii码的十进制表示为104,e的ascii码的十进制表示为101,以此类推
fmt.Printf("%b\n", bytes) // [1101000 1100101 1101100 1101100 1101111]
fmt.Printf("%b\n", s) // %!b(string=hello) wrong type
var u uint8 = 255
fmt.Println(u, u+1, u+2, u+3, u+4) // "255 0 1"
fmt.Printf("%b %b %b %b %b\n", u, u+1, u+2, u+3, u+4) // 11111111 10000000(截断存后8位 0) 10000001(截断存后8位 1) 10000010(截断存后8位 10) 10000011(截断存后8位 11)
// 最高位为 0 表示正数,最高位为 1 表示负数。
var i int8 = 127
// fmt.Println(i, i+1, i+2, i+3, i+4) // "127 -128 1"
fmt.Printf("%b %v\n", i+1, i+1) // 01111111 10000000(先计算,后截断存后8位。最高位符号位为1,变成负数) -1111111 -1111110 -1111101
// 128的二进制表示是10000000
// -128的二进制表示法:取补码:取反后得到01111111,再加1得到10000000。
}
|
两个相同的整数类型可以使用下面的二元比较运算符进行比较;比较表达式的结果是布尔类型。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| // 布尔型、数字类型和字符串等基本类型都是可比较的,也就是说**两个相同类型的值可以用==和!=进行比较**。
// 整数、浮点数和字符串可以根据比较结果排序
// 许多其它类型的值可能是不可比较的,因此也就可能是不可排序的。
== 等于
!= 不等于
< 小于
<= 小于等于
> 大于
>= 大于等于
// 一元的加法和减法运算符
// 对于整数,+x是0+x的简写,-x则是0-x的简写;对于浮点数和复数,+x就是x,-x则是x 的负数。
+ 一元加法(无效果)
- 负数
|
**bit位操作运算符:**移位操作的bit数部分必须是无符号数、被操作的x可以是有符号数或无符号数
- x«n左移运算 等价于 乘以 2^n,用0填充右边空缺的bit位
- x»n右移运算 等价于 除以 2^n,用0填充左边空缺的bit位
- 注意:有符号数的右移运算会用符号位的值填充左边空缺的bit位。(所以最好用无符号运算)
1
2
3
4
5
6
7
8
9
| // bit位操作运算符
& 位运算 AND
| 位运算 OR
^ 位运算 XOR // 作为二元运算符时是按位异或(XOR); 当用作一元运算符时表示按位取反,返回一个每个bit位都取反的数
&^ 位清空(AND NOT) // 按位置零(AND NOT)
// 前面4个操作运算符并不区分是有符号还是无符号数:
<< 左移
>> 右移
|
内置的len函数返回的为一个有符号的int(所以可以赋值为-1,能处理逆序循环),不能返回uint。
- 如果内置的len函数返回一个无符号数,i也将是无符号的uint类型。条件i >= 0则永远为真。i–语句将不会产生-1,而是溢出为uint类型的最大值 2^64-1,然后medals[i]表达式运行时将发生数组越界的panic异常。
- 所以,由于溢出问题,无符号数往往只有在位运算或其它特殊的运算场景才会使用,就像bit集合、分析二进制文件格式或者是哈希和加密操作等。它们通常并不用于仅仅是表达非负数量的场合。
1
2
3
4
| medals := []string{"gold", "silver", "bronze"}
for i := len(medals) - 1; i >= 0; i-- {
fmt.Println(medals[i]) // "bronze", "silver", "gold"
}
|
需要一个显式的转换将一个值从一种类型转化为另一种类型,并且算术和逻辑运算的二元操作中必须是相同的类型。(虽然这偶尔会导致需要很长的表达式,但消除了所有和类型相关的问题,提示了可读性)
类型转换通常不会改变数值,只是告诉编译器如何解释这个值。但对于将一个大尺寸的整数类型转为一个小尺寸的整数类型,或者是将一个浮点数转为整数(向0方向截断),可能会改变数值或丢失精度。
- Go风格采用排错性编程/防御性编程,你应该避免对可能会超出目标类型表示范围的数值做类型转换,因为截断的行为可能依赖于具体的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| // 以0开始:八进制格式,八进制数据通常用于POSIX操作系统上的文件访问权限标志。
o := 0666
// 以0x或0X开头:十六进制格式,十六进制数字则更强调数字值的bit位模式。
// Printf的**[1]副词**:%之后的[1]副词告诉Printf函数再次使用第一个操作数,不用再呆板的写多个同样的变量
// Printf的#副词:%后的#副词告诉Printf在用%o、%x或%X输出时生成0、0x或0X前缀。
fmt.Printf("%d %[1]o %#[1]o\n", o) // "438 666 0666"
x := int64(0xdeadbeef)
fmt.Printf("%d %[1]x %#[1]x %#[1]X\n", x)
// Output:
// 3735928559 deadbeef 0xdeadbeef 0XDEADBEEF
// 字符面值通过一对单引号直接包含对应字符
// 也可以通过转义的数值来表示任意的Unicode码点对应的字符
ascii := 'a'
unicode := '国'
newline := '\n'
fmt.Printf("%d %[1]c %[1]q\n", ascii) // "97 a 'a'"
fmt.Printf("%d %[1]c %[1]q\n", unicode) // "22269 国 '国'"
fmt.Printf("%d %[1]q\n", newline) // "10 '\n'"
|
1
2
3
4
5
6
7
8
9
10
11
| var compote = int(apples) + int(oranges)
f := 3.141 // a float64
i := int(f)
fmt.Println(f, i) // "3.141 3"
f = 1.99
fmt.Println(int(f)) // "1"
f := 1e100 // a float64
i := int(f) // 结果依赖于具体实现
|
浮点数
#
算术规范由IEEE754浮点数国际标准定义,该浮点数规范被所有现代的CPU支持;
float32类型的累计计算误差很容易扩散,能精确表示的正整数并不是很大,float32的**有效bit位只有23个****,**其它的bit位用于指数和符号;当整数大于23bit能表达的范围时,float32的表示将出现误差);
1
2
3
4
|
// float32
var f float32 = 16777216 // 1 << 24
fmt.Println(f == f+1) // "true"
|
很小或很大的数最好用科学计数法书写,通过e或E来指定指数部分:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
// 浮点数的字面值可以直接写小数部分:
const e = 2.71828 // (approximately)
// 小数点前面或后面的数字都可能被省略(如.707或1.)
const Avogadro = 6.02214129e23 // 阿伏伽德罗常数
const Planck = 6.62606957e-34 // 普朗克常数
// 用Printf函数的%g参数打印浮点数,将采用更紧凑的表示形式打印,并提供足够的精度
// 但对应表格的数据,使用%e(带指数)或%f的形式打印可能更合适。
// 都可以指定打印的宽度和控制打印精度。
for x := 0; x < 8; x++ {
fmt.Printf("x = %d e^x = %8.3f\n", x, math.Exp(float64(x))) // 3个小数精度和8个字符宽度
}
x = 0 e^x = 1.000
x = 1 e^x = 2.718
x = 2 e^x = 7.389
x = 3 e^x = 20.086
x = 4 e^x = 54.598
x = 5 e^x = 148.413
x = 6 e^x = 403.429
x = 7 e^x = 1096.633
|
math包提供了IEEE754浮点数标准中定义的特殊值的创建和测试:正无穷大 +Inf(太大溢出的数字)、 负无穷大 -Inf(除零的结果)、NaN非数(无效的除法操作结果0/0或Sqrt(-1))
1
2
| var z float64
fmt.Println(z, -z, 1/z, -1/z, z/z) // "0 -0 +Inf -Inf NaN"
|
math.IsNaN用于测试一个数是否是非数NaN,math.NaN则返回非数对应的值;虽然可以用math.NaN来表示一个非法的结果,但是测试一个结果是否是非数NaN则是充满风险的,因为NaN和任何数都是不相等的(译注:在浮点数中,NaN、正无穷大和负无穷大都不是唯一的,每个都有非常多种的bit模式表示):
1
2
3
4
5
6
7
8
9
10
11
| nan := math.NaN()
fmt.Println(nan == nan, nan < nan, nan > nan) // "false false false"
// 如果一个函数返回的浮点数结果可能失败,最好的做法是用单独的标志 ok bool 来报告失败,像这样:
func compute() (value float64, ok bool) {
// ...
if failed {
return 0, false
}
return result, true
}
|
example: surface
#
surface.go演示了通过浮点计算生成的图形。它是带有两个参数的z = f(x, y)函数的三维形式,使用了可缩放矢量图形(SVG)格式输出,SVG是一个用于矢量线绘制的XML标准。
图3.1显示了sin(r)/r函数的输出图形,其中r是sqrt(x*x+y*y)。

要解释这个程序是如何工作的需要一些基本的几何学知识:程序的本质是三个不同的坐标系中映射关系:
第一个是100x100的二维网格,对应整数坐标(i,j),从远处的(0,0)位置开始。我们从远处向前面绘制,因此远处先绘制的多边形有可能被前面后绘制的多边形覆盖。
第二个坐标系是一个三维的网格浮点坐标(x,y,z),其中x和y是i和j的线性函数,通过平移转换为网格单元的中心,然后用xyrange系数缩放。高度z是函数f(x,y)的值。
第三个坐标系是一个二维的画布,起点(0,0)在左上角。画布中点的坐标用(sx,sy)表示。我们使用等角投影将三维点(x,y,z)投影到二维的画布中。
画布中从远处到右边的点对应较大的x值和较大的y值。并且画布中x和y值越大,则对应的z值越小。x和y的垂直和水平缩放系数来自30度角的正弦和余弦值。z的缩放系数0.4,是一个任意选择的参数。
对于二维网格中的每一个网格单元,main函数计算单元的四个顶点在画布中对应多边形ABCD的顶点,其中B对应(i,j)顶点位置,A、C和D是其它相邻的顶点,然后输出SVG的绘制指令。
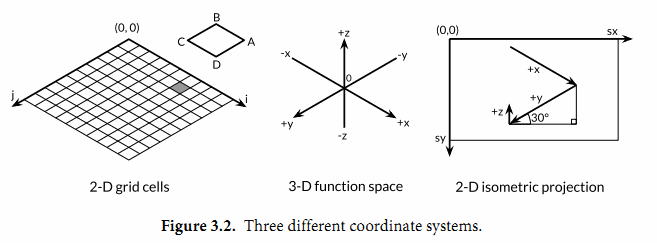
但是我们可以跳过几何学原理,因为程序的重点是演示浮点数运算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| // Surface computes an SVG rendering of a 3-D surface function.
// See page 58.
package main
import (
"fmt"
"io"
"log"
"math"
"net/http"
"os"
)
const (
width, height = 600, 320 // canvas size in pixels
cells = 100 // number of grid cells
xyrange = 30.0 // axis ranges (-xyrange..+xyrange)
xyscale = width / 2 / xyrange // pixels per x or y unit
zscale = height * 0.4 // pixels per z unit
angle = math.Pi / 6 // angle of x, y axes (=30°)
)
var sin30, cos30 = math.Sin(angle), math.Cos(angle) // sin(30°), cos(30°)
func main() {
if len(os.Args) > 1 && os.Args[1] == "web" {
handler := func(w http.ResponseWriter, r *http.Request) {
// 设置Content-Type头部为"image/svg+xml",表示响应的内容类型为SVG图像
w.Header().Set("Content-Type", "image/svg+xml")
surface(w)
}
fmt.Println("start web server http://localhost:8000")
http.HandleFunc("/", handler)
log.Fatal(http.ListenAndServe("localhost:8000", nil))
}
surface(os.Stdout)
}
// 入参 out io.Writer 表示输出的目的地
func surface(out io.Writer) {
fmt.Fprintf(out, "<svg xmlns='http://www.w3.org/2000/svg' "+
"style='stroke: grey; fill: white; stroke-width: 0.7' "+
"width='%d' height='%d'>", width, height)
for i := 0; i < cells; i++ {
for j := 0; j < cells; j++ {
ax, ay := corner(i+1, j)
bx, by := corner(i, j)
cx, cy := corner(i, j+1)
dx, dy := corner(i+1, j+1)
fmt.Fprintf(out, "<polygon points='%g,%g %g,%g %g,%g %g,%g'/>\n",
ax, ay, bx, by, cx, cy, dx, dy)
}
}
fmt.Fprintf(out, "</svg>")
}
func corner(i, j int) (float64, float64) {
// Find point (x,y) at corner of cell (i,j).
x := xyrange * (float64(i)/cells - 0.5)
y := xyrange * (float64(j)/cells - 0.5)
// Compute surface height z.
z := f(x, y)
// Project (x,y,z) isometrically onto 2-D SVG canvas (sx,sy).
sx := width/2 + (x-y)*cos30*xyscale
sy := height/2 + (x+y)*sin30*xyscale - z*zscale
return sx, sy
}
func f(x, y float64) float64 {
r := math.Hypot(x, y) // distance from (0,0)
return math.Sin(r) / r
}
|
复数
#
复数在几何上可以表示为平面上的点,实部表示点在x轴上的坐标,虚部表示点在y轴上的坐标。
复数的加法和减法对应于平面上点的平移,而复数的乘法和除法对应于平面上点的旋转和缩放。
复数在物理学中的具体应用:
- 波动现象:在波动现象中,复数通常用来表示波的振幅和相位。例如,在描述电磁波(如光)时,电场和磁场可以用复数表示,其中实部表示场的振幅,虚部表示场的相位。
- 量子力学:复数是描述量子态的基本工具。量子态可以用波函数表示,而波函数通常是一个复数函数。波函数的模平方表示在某个位置找到粒子的概率密度,而波函数的相位则包含了粒子的量子力学信息,如动量和能量。
- 电路分析:复数用来表示交流电路中的电压和电流。
- 信号处理:复数表示信号的幅度和相位。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| // 内置的complex函数用于构建复数,内建的real和imag函数分别返回复数的实部和虚部
var x complex128 = complex(1, 2) // 1+2i
var y complex128 = complex(3, 4) // 3+4i
fmt.Println(x*y) // "(-5+10i)"
fmt.Println(real(x*y)) // "-5"
fmt.Println(imag(x*y)) // "10"
// 如果一个浮点数面值或一个十进制整数面值后面跟着一个i,例如3.141592i或2i,它将构成一个复数的虚部,复数的实部是0:
fmt.Println(1i * 1i) // "(-1+0i)", i^2 = -1
上面x和y的声明语句还可以简化:
x := 1 + 2i
y := 3 + 4i
// 复数也可以用==和!=进行相等比较。
// 只有两个复数的实部和虚部都相等的时候它们才是相等的(译注:浮点数的相等比较是危险的,需要特别小心处理精度问题)。
// math/cmplx包提供了复数处理的许多函数,例如求复数的平方根函数和求幂函数。
fmt.Println(cmplx.Sqrt(-1)) // "(0+1i)"
|
example: mandelbrot
#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
| // Mandelbrot emits a PNG image of the Mandelbrot fractal.
// See page 61.
package main
import (
"fmt"
"image"
"image/color"
"image/png"
"io"
"log"
"math/cmplx"
"net/http"
"os"
)
func main() {
if len(os.Args) > 1 && os.Args[1] == "web" {
handler := func(w http.ResponseWriter, r *http.Request) {
// 设置Content-Type头部为"image/svg+xml",表示响应的内容类型为SVG图像
genImg(w)
w.Header().Set("Content-Type", "image/png")
}
fmt.Println("start web server http://localhost:8000...")
http.HandleFunc("/", handler)
log.Fatal(http.ListenAndServe("localhost:8000", nil))
return
}
genImg(os.Stdout)
}
func genImg(out io.Writer) {
// 定义图像的边界和尺寸
const (
// 图像 x 轴的最小值
xmin, ymin, xmax, ymax = -2, -2, +2, +2
// 图像的宽度和高度(像素)
width, height = 1024, 1024
)
// 创建一个新的 RGBA 图像
img := image.NewRGBA(image.Rect(0, 0, width, height))
// 遍历图像的每个像素
for py := 0; py < height; py++ {
// 将像素的 y 坐标转换为对应的复数的实部
y := float64(py)/height*(ymax-ymin) + ymin
for px := 0; px < width; px++ {
// 将像素的 x 坐标转换为对应的复数的虚部
x := float64(px)/width*(xmax-xmin) + xmin
// 构建复数
z := complex(x, y)
// 将像素 (px, py) 设置为对应复数 z 的 Mandelbrot 颜色
img.Set(px, py, mandelbrot(z))
}
}
// 将图像编码为 PNG 格式并输出到标准输出流
png.Encode(out, img) // NOTE: ignoring errors
}
// mandelbrot 函数用于计算并返回 Mandelbrot 集合中对应于复数 z 的颜色
func mandelbrot(z complex128) color.Color {
// 定义迭代次数和对比度
const iterations = 200
const contrast = 15
// 初始化变量 v 为 0
var v complex128
// 迭代计算 v 的值
for n := uint8(0); n < iterations; n++ {
// 更新 v 的值,v 的平方加上输入的复数 z
v = v*v + z
// 如果 v 的模长大于 2,则认为该点逃逸出 Mandelbrot 集合
if cmplx.Abs(v) > 2 {
// 返回一个灰色值,其亮度与迭代次数成反比
return color.Gray{255 - contrast*n}
}
}
// 如果迭代结束后 v 的模长仍未超过 2,则认为该点属于 Mandelbrot 集合,返回黑色
return color.Black
}
// Some other interesting functions:
// acos 函数计算复数 z 的反余弦值,并将结果映射到颜色空间
func acos(z complex128) color.Color {
// 计算 z 的反余弦值
v := cmplx.Acos(z)
// 将反余弦值的实部映射到蓝色通道
blue := uint8(real(v)*128) + 127
// 将反余弦值的虚部映射到红色通道
red := uint8(imag(v)*128) + 127
// 返回一个 YCbCr 颜色,其中 Y 分量设置为 192,Cb 和 Cr 分量分别由蓝色和红色值确定
return color.YCbCr{192, blue, red}
}
// sqrt 函数计算复数 z 的平方根,并将结果映射到颜色空间
func sqrt(z complex128) color.Color {
// 计算 z 的平方根
v := cmplx.Sqrt(z)
// 将平方根值的实部映射到蓝色通道
blue := uint8(real(v)*128) + 127
// 将平方根值的虚部映射到红色通道
red := uint8(imag(v)*128) + 127
// 返回一个 YCbCr 颜色,其中 Y 分量设置为 128,Cb 和 Cr 分量分别由蓝色和红色值确定
return color.YCbCr{128, blue, red}
}
// f(x) = x^4 - 1
//
// z' = z - f(z)/f'(z)
//
// = z - (z^4 - 1) / (4 * z^3)
// = z - (z - 1/z^3) / 4
//
// newton 函数使用牛顿迭代法来逼近方程 f(x) = x^4 - 1 的根,并将迭代次数映射到颜色空间
func newton(z complex128) color.Color {
// 定义迭代次数和对比度
const iterations = 37
const contrast = 7
// 迭代更新 z 的值
for i := uint8(0); i < iterations; i++ {
// 使用牛顿迭代公式更新 z 的值
z -= (z - 1/(z*z*z)) / 4
// 如果 z 的四次方与 1 的差的绝对值小于 1e-6,则认为找到了一个根
if cmplx.Abs(z*z*z*z-1) < 1e-6 {
// 返回一个灰色值,其亮度与迭代次数成反比
return color.Gray{255 - contrast*i}
}
}
// 如果没有找到根,则返回黑色
return color.Black
}
|

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
i := 0
if b {
i = 1
}
// 如果需要经常做类似的转换,包装成一个函数会更方便:
func btoi(b bool) int {
if b {
return 1
}
return 0
}
// 数字到布尔型的逆转换则非常简单,不过为了保持对称,我们也可以包装一个函数:
// itob reports whether i is non-zero.
func itob(i int) bool { return i != 0 }
|


